![[파이썬을 활용한 통계 개념 기초] 12. 표본 및 통계(Sample & statistic)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FcxYdY6%2FbtsKwmKXcKv%2Fw3kaA03nJfYx2egGki4YhK%2Fimg.png)

표본 및 통계
모집단과 표본
- 모집단(Population)은 연구의 관심 대상이 되는 전체 집단을 의미합니다. 예를 들어, 한국 20대가 특정 색상을 얼마나 좋아하는지 알고 싶다면, 한국 20대 전체가 모집단이 됩니다. 모집단은 우리가 연구하고자 하는 모든 대상이 포함된 집합으로, 이 안의 특성을 정확하게 파악할 수 있다면 모집단에 대해 확실한 결론을 내릴 수 있습니다.
- 하지만 현실적으로 모든 개체를 조사하는 것은 불가능하거나 비효율적일 수 있습니다. 그래서 모집단의 특성을 추정하기 위해 일부 개체를 선택한 표본(Sample)을 사용합니다. 표본은 모집단을 대표할 수 있도록 선택해야 하며, 확률 표본(Random Sample)을 사용하는 것이 일반적입니다. 확률 표본을 통해 모집단의 모든 개체가 동일한 확률로 선택될 수 있게 하여 표본이 모집단을 잘 대표하도록 합니다.
확률 표본의 독립성
표본을 구성하는 각 관측값 X1,X2,…,Xn은 서로 독립적이고 동일한 분포를 따라야 합니다.
즉, 각 관측값이 다른 값에 영향을 받지 않으며 동일한 확률 분포를 따라야 합니다. 이러한 독립성 가정은 많은 통계적 추론의 기초가 되며 모집단의 특성을 일관되게 추정할 수 있게 합니다.
예를 들어, 어떤 날의 날씨와 주가 데이터를 동시에 표본으로 사용한다면, 날씨와 주가는 서로 영향을 주고받는 관계에 있을 수 있으므로 완전히 독립적이지 않다고 할 수 있습니다. 따라서 두 변수 간의 관계가 없는 독립적 표본을 수집해야만 모집단의 특성을 정확히 반영할 수 있습니다. 이러한 독립성 가정은 모집단에 대한 일관된 추론을 가능하게 합니다.
표본 평균과 기댓값
표본 평균(Sample Mean)은 표본 관측값의 평균을 나타내며, 모집단의 평균을 추정하는 데 사용됩니다.
표본 평균은 다음과 같이 계산됩니다.

이 값은 모집단의 기댓값(Expectation)을 추정하는 역할을 합니다. 기댓값은 모집단 전체의 평균적인 경향을 나타내는 이론적 값인 반면, 표본 평균은 실제 관측된 값들의 평균으로, 통계량(statistic)이라고 합니다. 따라서 표본 평균은 모집단의 기댓값을 추정하는데 사용되며, 이 과정에서 통계적 추론을 통해 모집단에 대해 결론을 내릴 수 있습니다.
표본 분산
표본 분산(Sample Variance)은 표본 데이터가 평균값에서 얼마나 퍼져 있는지를 나타냅니다.
표본 분산은 다음과 같은 공식으로 계산됩니다:
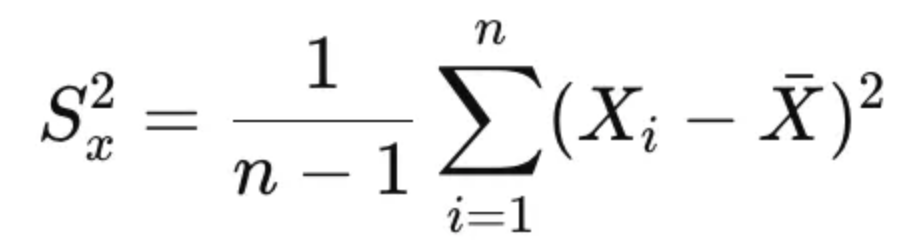
여기서 n−1로 나누는 이유는 베셀의 보정(Bessel’s correction)이라 불리는 것으로, 모집단 분산을 추정할 때 생기는 편향을 보정하기 위함입니다. 이 보정을 통해 표본 분산이 모집단 분산의 불편 추정량이 됩니다.
여기서 n−1로 나누는 이유는 베셀의 보정(Bessel’s correction) 때문입니다. 이는 표본으로부터 모집단의 분산을 추정할 때 생기는 편향을 보정하기 위한 방법입니다. 단순히 n으로 나눌 경우, 표본 분산이 모집단 분산을 과소추정할 수 있기 때문에 n−1로 나누어 추정치를 더 정확하게 만듭니다. 이를 통해 표본 분산이 모집단 분산의 불편 추정량이 되며, 통계적으로 모집단의 실제 분산을 더 잘 반영할 수 있습니다.
통계량과 모수
- 통계량(Statistic)은 표본 데이터를 이용해 계산된 값(예: 표본 평균 , 표본 분산)으로, 이는 모집단의 모수(Parameter)를 추정하는 데 사용됩니다.
- 여기서 중요한 차이는, 모수는 주어진 모집단에 대해 고정된 값이지만, 통계량은 표본에 따라 변동하는 값이라는 점입니다.
- 모수(Parameter)는 모집단의 고정된 특성을 나타내는 값으로, 모집단의 평균(μ)이나 분산(σ²) 같은 값들이 모수에 해당합니다. 모수는 모집단 전체를 대상으로 정의된 값이기 때문에 일정하지만, 통계량은 표본에 따라 달라질 수 있습니다. 따라서 통계량은 표본에 의존하는 값이며, 표본이 달라질 때마다 그 값도 변동합니다.
'통계 > 파이썬을 이용한 통계 기초' 카테고리의 다른 글
| [파이썬을 활용한 통계 개념 기초] 14. 카이제곱 분포(Chi-squared distribution) (1) | 2024.11.22 |
|---|---|
| [파이썬을 활용한 통계 개념 기초] 13. F 분포와 t 분포(F and t distribution) (0) | 2024.11.19 |
| [파이썬을 활용한 통계 개념 기초] 11. 독립(Independence) (0) | 2024.10.31 |
| [파이썬을 활용한 통계 개념 기초] 10. 기댓값(Expectation) (1) | 2024.10.24 |
| [파이썬을 활용한 통계 개념 기초] 09. 음이항 분포(Negative binomial distribution) (1) | 2024.10.17 |

데이터 분석을 공부하고 카페를 열심히 돌아다니는 이야기
포스팅이 좋았다면 "좋아요❤️" 또는 "구독👍🏻" 해주세요!
![[파이썬을 활용한 통계 개념 기초] 11. 독립(Independence)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FDiF8w%2FbtsKopup8qh%2Fpo8bd8PlNON8EViXjVeyMk%2Fimg.png)
![[파이썬을 활용한 통계 개념 기초] 10. 기댓값(Expectation)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FnBMlZ%2FbtsKgB8PX0n%2FQIrQlgPDQizWigiO2hya81%2Fimg.png)